Reinforcement learning has recently been succeeded to go over the human's ability in video games and Go. This implies possiblities to beat human's performance in other fields where human is doing well. Stock trading can be one of such fields. Some professional In this article, we consider application of reinforcement learning to stock trading. Especially, we work on constructing a portoflio to make profit. Since portfolio can take inifinite number, we tackle this task based on Deep Deterministic Policy Gradient (DDPG). The behavior of stock prices is konwn to depend on history and several time scales, which leads us to use multiscale CNN for Q and actor network. We show that our algorithm has better performance than monkey trading(taking actions at random).

1. Background¶

Reinforcement learning is one of categories of machine learning method along with unsupervised and supervised learning. This learning framework has recently been succeeded to go over the human's ability in some fields. Algorithms find patters and best performance actions from received signals as well as we do in our daily life. The performance of action is evaluated through reward signals;, i.e., the action to maximize reward signals is considered as the best one. In this section, we review recent development of Q-learning and its variation with neural network. If you want to learn this topic deeply, I highly recommend you to read this book.

Q-Learning¶

Q-learning is a method based on temporal difference learning(TDL), which results from the combination of Dynamic Programming(DP) ideas and Monte Carlo(MC) ideas.

Let $Q(s, a)$ be an $\mathbb{R}$ valued function taking state $s$ and action $a$ as input, i.e., $Q(s, a)$ is a function to estimate the value of a pair $(s, a)$. With respect to a policy $\pi$, we can evaluate the value of state $s$ as $$V_{\pi}(s) = E_{\pi} [Q(s, \cdot)] = \int P_{\pi}(da | s) Q(s, a), $$ where $P_{\pi}(da | s)$ is conditional probability of action given state $s$. $V_{\pi}(s)$ evaluates the value of state $s$ under the policy $\pi$. Everytime taking action, the environment gives you reward $r_t$. With decay rate $0 < \gamma \leq 1$, we define the total reward as $$R_t = \sum_{s=0}^\infty \gamma^s r_{t+s}$$ Then, we obtain $$V_{\pi}(s_t) = E_{\pi}[R_t]$$ $$= E_{\pi}[r_t + \gamma R_{t+1}]$$ $$= E_{\pi} [r_t + \gamma V_{\pi}(s_{t+1})]$$ Since we use maximal operator $\pi$ in Q-learning, we have $$Q(s_t, a_t) = E[r_t + \gamma \underset{a}{max} Q_{\theta}(s_{t+1}, a)],$$ where $a_t$ is action chosen by the behavior policy at $t$. This is one of the Bellman equations, which is fundamental equation of DP.

To optimize function to satisfy above identity as much as possible, we use $\alpha-MC$. For each $(s_t, a_t)$, we have the following update: $$Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha E[r_t + \gamma \underset{a}{max} Q_{\theta}(s_{t+1}, a) - Q(s_t, a_t)].$$ Note that when $\alpha = \frac{1}{n}$, this is equivalent to the normal MC method. $$Q^n(s_t, a_t) = \frac{1}{n}[\sum_{i=1}^nR_t^i]$$ $$= \frac{1}{n}[R_t^1 + (n - 1)\frac{1}{n - 1}\gamma \sum_{i=2}^nR_{t}^i]$$ $$= \frac{1}{n}[R_t^1 + (n - 1)Q^{n-1}(s_t, a_t)]$$ $$= Q^{n-1}(s_t, a_t) + \frac{1}{n}[R_t^1 - Q^{n-1}(s_t, a_t)]$$

Q-learning frame work does not require you to wait for updating parameters until getting truth value $R_t$. Thus, Q-learning is suited for online-learning.

DQN¶

In vanilla Q-learning, we used $\alpha-MC$ for updating parameters. This method, however, is effective only with the lower dimensional input state. We have to consider different approaches for the case with high or infinite dimensional input; e.g., real value input. As one of the approaches, we can use neural network for Q-function. This method is introduced as Deep Q-Network(DQN). Instead of $\alpha-MC$, we use gradient descent method to update parameters; i.e., we minimize the following loss function: $$L_{\theta} = [r_t + \gamma \underset{a}{max} Q_{\theta}(s_{t+1}, a) - Q_{\theta}(s_{t}, a_t) ]^2.$$ For detail, you can check the original paper.

DDPG¶

For some tasks like car driving and playing sports, we have high or infinite dimensional action space, which makes it difficult for maximal operator to be used. Then, we introduce neural network to determine action, policy network, instead of maximal operator. This network learns optimal action through parameter optimization like gradient descent. Let $A_{\tilde{\theta}}$ be a policy network. Then, we have the following loss function, $$L_{\theta, \tilde{\theta}} = [r_t + \gamma Q_{\theta}(s_{t+1}, A_{\tilde{\theta}}(s_{t+1})) - Q_{\theta}(s_{t}, a_t) ]^2.$$ For detail, you can check Deep Deterministic Policy Gradient(DDPG).

2. Reinforcement Learninig for Stock Trading¶

In the previous section, we introduce Q-learning and its extensions with neural network. We now move to considering application of Q-learning to stock trading.

Framework¶

One of the most important goals of stock trading is making profit through selling downtrend stocks and buying uptrend stocks. The profit is basically determined by components of the portfolio -- a group of stocks -- and the behavior of stock prices. For instance, if you buy 3 units of stock A and its price goes up 20 dollars higher, you get $3 \times 20$ dollars profit.

With this in mind, the algorithm should be designed to construct a portfolio that maximize the profit. Reward here corresponds to the profit made by the portfolio; i.e. the difference between current and past portfolio value. Thus, we can write down as $$r_t = Port(s_{t+1} | \theta_t) - Port(s_t | \theta_t),$$ where $r_t$ and $s_t$ are reward and stock prices at $t$; $\theta_t$ is weight parameters of a portfolio at $t$ -- how many each stock to hold determined at $t$; $Port(\cdot | \theta_t)$ is a portfolio value function of stock prices given weight parameters $\theta_t$. In this framework, constructing an optimal portfolio is equivalent to finding $\theta_t$ to make the most profit, i.e., we guess $s_{t+1}$ and find $\theta_t$ that maximize $r_t$ for each time $t$.

Next, we consider the network architecture. Since there are infinite number of allowed values for weight parameters of a portfolio, we employ DDPG, which uses two network: Q-network and actor network. Let us assume that we construct a portfolio consisting of $n$ stocks. Q-network takes $n$ portfolio weight parameters and $n$ stock prices as input and then produce the value. We can write down as $$f_{Q}:\mathbb{R}^n \times\mathbb{R}^n \to \mathbb{R}.$$ The output of the actor network corresponds to the portfolio weight parameters. Though weight parameters practically have to be integers, we take $\mathbb{R}^{n}$ as action space. Thus, we define as $$f_{actor}:\mathbb{R}^n \to \mathbb{R}^{n}. $$

We shall specify the type of networks to use. Professional traders often predict the behavior of stock prices based on techinical indicators, which includes moving average, exponential moving average, MACD, etc. Especially, some combinations of different time scale indicators like the golden cross are consider to be effective. To introduce this intuition, we use multiscale CNN for both of the Q-network and the actor network.

Experimental Results¶

We here consider constructing a portfolio with the 10 biggest volume companies out of 500 stocks used for Standard and Poor's 500. The figure below shows chosen stocks and their volume.

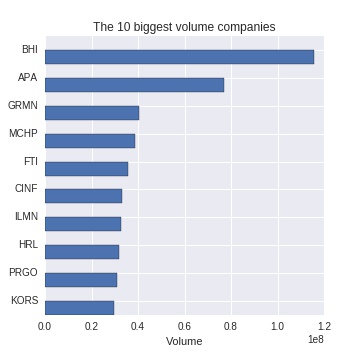
We compare the performance with other algorithms: randomly chosen portfolio.

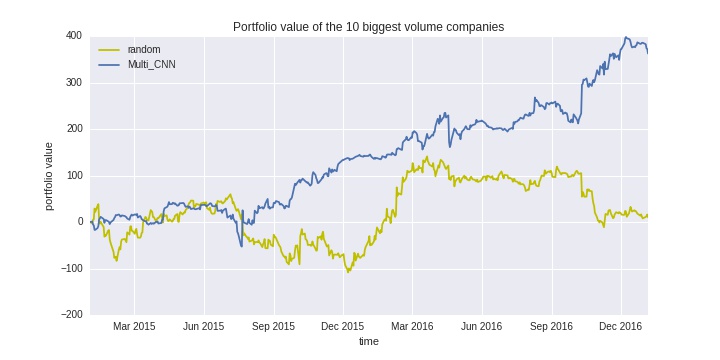
In the above graph, we have two results: ‘Multi_CNN’ and ‘random’. Since performances fluctuate, we evalute algorithms with 10 sample mean. ‘Multi_CNN’ corresponds to the result of the algorithm we develop in this article. Randomly chosen portfolio — ‘random’ in the graph — follows the normal distribution $N(0, 5 \cdot \bf{I_n})$, where $\bf{I_n}$ is n-dimensional identity matrix. Multi scale CNN perfumes better and random one just wanders around zero. This implies the effectiveness of multi scale CNN along with the fact that managing portfolio at random does not make any profit.

3. Discussion¶

We have discussed how to apply reinforcement learning to stock trading and have developed framework with DDPG. To realize the intuition of professional traders, we multi use scale CNN, which results in better performance than randomly chosen portfolio.

Since we allow the algorithm to short sell and portfolio is expressed as real numbers, we have to introduce some conditions for applying to real stock trading.